논문 제출일자: 2023년 10월 14일
[논문 원문 링크]
시계열 예측은 리테일, 금융, 제조업, 의료, 자연과학 분야에서 두루두루 필요한 분야입니다. 시계열 예측은 딥러닝 모델들이 완전히 정복하지 못한 분야로 아직까지 ARIMA, GARCH 같은 전통적인 통계학적 접근 방법을 이용한 도구가 좋은 성능을 보이고 있습니다. 이 논문에서는 현재까지의 SOTA 모델들과 견주어 볼 만한 트랜스포머 아키텍쳐 기반의 딥러닝 모델 TimesFM을 소개합니다.
자연어 처리(NLP) 분야에서는 대규모 언어 모델(LLM)이 대규모 데이터셋으로 학습되어 다양한 다운스트림 태스크에서도 뛰어난 성능을 발휘하고, 때때로 준수한 제로샷 성능을 보입니다. 이는 "대규모 시계열 데이터로 사전학습된 모델이 이전에 보지 못한 데이터셋의 시계열 예측에 유용한 시간적 패턴을 학습할 수 있을까?" 라는 궁금증을 자아냅니다.
TimesFM 소개: 시계열 예측을 위한 파운데이션 모델
TimesFM은 LLM에서 영감을 받아 시계열 예측을 위해 설계된 파운데이션 모델입니다. 파라미터 크기(200M)와 사전 학습 데이터 양(O(100B) 타임포인트)은 LLM 보다 작지만, TimesFM은 개별 데이터셋에 맞춰 지도 학습된 최신 모델과 동급의 제로샷 성능을 보여줍니다.
TimesFM의 핵심
- 합성 데이터 사용: 대규모 데이터를 얻기 위해 실제 데이터(예: 구글 트렌드, 위키미디어 페이지뷰)와 합성 데이터를 활용하여 다양한 학습 데이터 확보
- 디코더 모델: 다양한 컨텍스트 길이를 입력받고 예측 호라이즌을 처리할 수 있도록 패칭을 이용한 디코더 어텐션 아키텍쳐를 설계
모델 아키텍쳐 이해하기
Patching
TimesFM은 시계열 데이터를 패치 단위로 나누어 처리합니다. NLP의 토큰과 유사하며, 패칭을 하지 않을 때와 비교해서 토큰의 수가 1/패치 길이 만큼 토큰 수가 줄어듭니다. 그러나 패치 길이를 너무 길게 늘리면 디코더 모델로 학습이 어려워지게 됩니다.
Decoder-Only Model
TimesFM은 디코더 모델에서 학습되어 이전 패치들을 기반으로 다음 패치를 예측하도록 학습됩니다(GPT의 next token prediction과 비슷). LLM과 유사하게 병렬 학습이 가능하고 다양한 길이의 입력을 통해 미래 패치를 예측 하는 능력을 얻게됩니다.
Longer Output Patches
TimesFM은 의도적으로 입력 시퀀스 길이보다 긴 출력 시퀀스를 예측하도록 설계되어 있습니다. 최근 연구에 따르면 긴 출력 시퀀스를 예측 할 때 자기회귀(autoregressive) 방식으로 예측하는 것 보다 한번에! 통으로! 예측하는 것이 예측 오차율이 낮습니다. 왜냐하면 데이터의 전체적인 패턴을 더 잘 포착할 수 있고 자기회귀 방식은 오류가 누적되기 때문입니다.
Patch Masking
논문에서는 패치 길이를 32, 64, 96, ...과 같이 32의 배수로 둡니다. 그러나 패치를 그대로 사용하면 패치 길이의 배수가 되는 컨텍스트에 대해서만 잘 예측하게 될 수 있습니다. 마스킹을 적절히 섞어 다양한 길이의 컨텍스트로 학습할 수 있도록 합니다
모델 구성 요소
Input Layers
입력 패치를 입력 토큰으로 바꾸는 역할을 합니다. 시계열 데이터를 연속되고 겹치지 않도록 패치 단위로 자르고 Residual block에 의해 크기가 `model_dim`인 벡터로 변환됩니다. 입력 토큰과 함께 이진 패딩 마스크 $m_{1:L}$이 같이 립력됩니다. 이 때, 1이면 마스킹이 되고 0이면 마스킹 되지 않습니다.
입력 $\mathbf{y}_{1: L}$은 크기가 $p$인 패치들로 나뉘게 되고 $j$-번째 패치는 $\tilde{\mathbf{y}}_j=\mathbf{y}_{p(j-1)+1: p j}$로 표현됩니다. 마찬가지로 마스크도 $\tilde{\mathbf{m}}_j=\mathbf{m}_{p(j-1)+1: p j}$로 표현됩니다.
따라서 트랜스포머 레이어에 들어가는 $j$-번째 입력 토큰은 다음과 같이 표현됩니다:
$$\mathbf{t}_j= \texttt{InputResidualBlock}\left(\tilde{\mathbf{y}}_j \odot\left(1-\tilde{\mathbf{m}}_j\right)\right)+\mathrm{PE}_j$$
여기서 $PE_j$는 $j$-번째 포지셔널 인코딩을 나타냅니다. 포지셔널 인코딩은 "Attention is All You Need" 논문에서와 같은 방법을 사용했습니다.
Stacked Transformer
모델 파라미터의 대부분은 여러 겹의 트랜스포머 층에 있습니다. 각 층은 multi-head self-attention과 그 뒤에 FFN 이 붙은 구조입니다. $j$-번째 출력 토큰은 다음과 같이 표현 될 수 있습니다:
$$\mathbf{t}_j= \texttt{InputResidualBlock}\left(\tilde{\mathbf{y}}_j \odot\left(1-\tilde{\mathbf{m}}_j\right)\right)+\mathrm{PE}_j$$
여기서 $\dot{m}_j$는 패치 내 모든 타임 포인트가 마스킹 되어있으면 1 아니면 0이 됩니다.
Output Layers
언어모델처럼 출력 토큰이 마지막 입력 패치의 다음 패치를 예측할 수 있어야합니다. 언어모델과의 차이점이라면 입력 패치와 출력 패치의 크기가 같지 않다는 것입니다. 아까 말씀드렸던 것 처럼 입력 패치보다 긴 길이를 예측하도록 설계되었기 때문입니다. 출력 패치의 길이를 `output_patch_len`$(h)$라고 합니다. 출력 토큰은 output residual block을 거쳐 출력 패치가 됩니다. 예측된 출력 패치는 다음과 같이 표현됩니다:
$$\hat{\mathbf{y}}_{p j+1: p j+h}= \texttt{OutputResidualBlock}\left(\mathbf{o}_j\right)$$
Loss Function
이 모델은 포인트 예측에 초점을 맞췄기 때문에 Mean Squared Error 같은 포인트 예측 오차 함수를 사용합니다
$$\texttt{TrainLoss} =\frac{1}{N} \sum_{j=1}^N \operatorname{MSE}\left(\hat{\mathbf{y}}_{p j+1: p j+h}, \mathbf{y}_{p j+1: p j+h}\right)$$
확률적 예측을 하고자 한다면 다중 출력 헤드(multiple output heads)를 두어 각 헤드가 분위수 오차를 줄이는 형태로 할 수 있습니다. 또 다른 방법으로는 확률 분포의 파라미터를 출력(예를 들어, 평균과 표준편차)해서 최대우도추정(MLE)를 사용해 손실을 계산할 수 있습니다
Training
이 논문에서는 모델 학습을 위해 표준적인 미니배치 경사하강법을 사용했습니다. 다만 표준과 다른 부분은 마스크를 샘플링 하는 방법입니다. LLM에서의 마스킹은 전체 시퀀스에서 완전히 랜덤한 인덱스를 추출하여 마스킹합니다. 하지만 여기서는 순서가 중요한 시계열 데이터를 사용하기 때문에 맨 앞 r개의 연속된 시퀀스가 마스킹 되는 방식입니다.
각 시계열에 대해 $0$부터 $p-1$($p$는 패치의 길이)사이의 값 $r$을 랜덤하게 뽑은 후 -> $m_{1:r} = 1$로 설정하고 나머지는 0으로 둡니다 -> 결과적으로 첫 번째 패치에서 첫 $r$개의 시퀀스는 마스킹 됩니다. 따라서 1부터 전체 길이까지 모든 길이를 커버할 수 있습니다.
Inference
추론 단계에서는 $\mathbf{y}_{1:L}$을 입력으로 받아 $\hat{\mathbf{y}}_{L+1:L+h}$를 예측합니다. 다음으로 이전 이전 타임스텝의 입력과 출력을 이어붙인 $\tilde{\mathbf{y}}_{1: L+h}=\left[\mathbf{y}_{1: L} ; \hat{\mathbf{y}}_{L+1: L+h}\right]$를 이용해 $\hat{\mathbf{y}}_{L+h+1: L+2 h}$를 예측합니다. 만약 $L$이 $p$의 배수가 아니면 $0$을 이어붙여 배수로 만들어준 후 마스킹해주게 됩니다. 학습 단계에서는 예측하는 길이가 점차 늘어나지만 추론 단계에서는 예측하는 horizon length $(h)$가 일정합니다. 혼동에 주의하세요!
사전 학습 데이터와 모델 구성
데이터 출처
Google Trends
- 2007년부터 2022년까지 15년간의 검색 관심도 데이터를 기반으로 22,000개의 주요 검색어를 선택했습니다.
- 검색어 관심도는 시간별, 일별, 주별, 월별로 나누어 수집했습니다.
- 대략 5억 개의 시간 포인트 데이터가 사용되었습니다.
Wiki Pageviews
- 2012년 1월부터 2023년 11월까지의 위키미디어 페이지 조회수를 수집했습니다.
- 시간 단위, 일 단위, 주 단위, 월 단위로 데이터를 집계하고, 3000억 개의 시간 포인트 데이터를 확보했습니다.
합성 데이터
- ARMA 프로세스, 계절성 패턴, 트렌드, 계단 함수 등을 결합하여 합성 데이터를 생성했습니다.
- 각각 2048 시간 포인트로 구성된 300만 개의 합성 시계열 데이터를 만들었습니다.
기타 실제 데이터
- M4 데이터셋: 10만 개의 시계열 데이터.
- 전기 사용량 및 교통량 데이터셋: 각각 800개 이상, 300개 이상의 시계열 데이터.
- 기상 데이터셋: 10분 단위 데이터.
데이터 혼합 및 학습
- 데이터 로더는 실제 데이터와 합성 데이터를 8:2 비율로 샘플링합니다.
- 모든 시간 세분성 그룹(시간 단위, 일 단위, 주 단위, 월 단위 이상)이 같은 파라미터를 공유합니다.
- 최대 컨텍스트 길이는 512로 설정되었으며, 주 단위는 256, 월 단위 이상은 64로 설정되었습니다.
- 각 시계열의 컨텍스트는 첫 번째 패치의 평균과 표준 편차를 사용해 스케일링했습니다.
실증적 결과
제로샷 평가
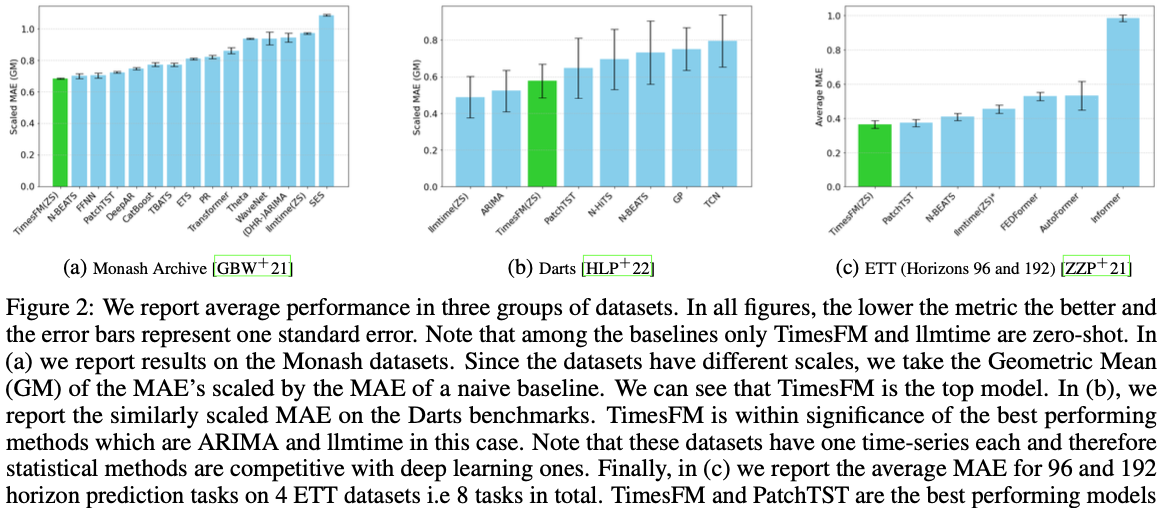
Monash 데이터셋
- 금융, 수요 예측, 기상, 교통 데이터를 포함한 30개의 데이터셋 중 18개를 사용했습니다.
- ARIMA, ETS, CatBoost, DeepAR, WaveNet 등과 성능을 비교했습니다.
- 데이터셋 간 값의 차이가 크기 때문에 naive baseline의 메트릭으로 정규화된 MAE를 기하평균으로 계산했습니다.
Darts 데이터셋
- 계절성과 가법적 및 승법적 경향을 가지는 8개의 단변량 데이터셋을 사용했습니다.
- 8개 데이터셋의 정규화된 MAE를 기하평균하여 성능을 평가했습니다.
Informer 데이터셋
- 1시간 단위와 15분 단위의 변압기 온도(전기 사용량) 변화를 포함하는 데이터셋을 사용했습니다.
- rolling validation 대신 마지막 테스트 윈도우에서 성능을 비교했습니다.
- 데이터셋이 이미 표준화되어 있으므로 MAE를 그대로 평균 냈습니다.
어블레이션 연구
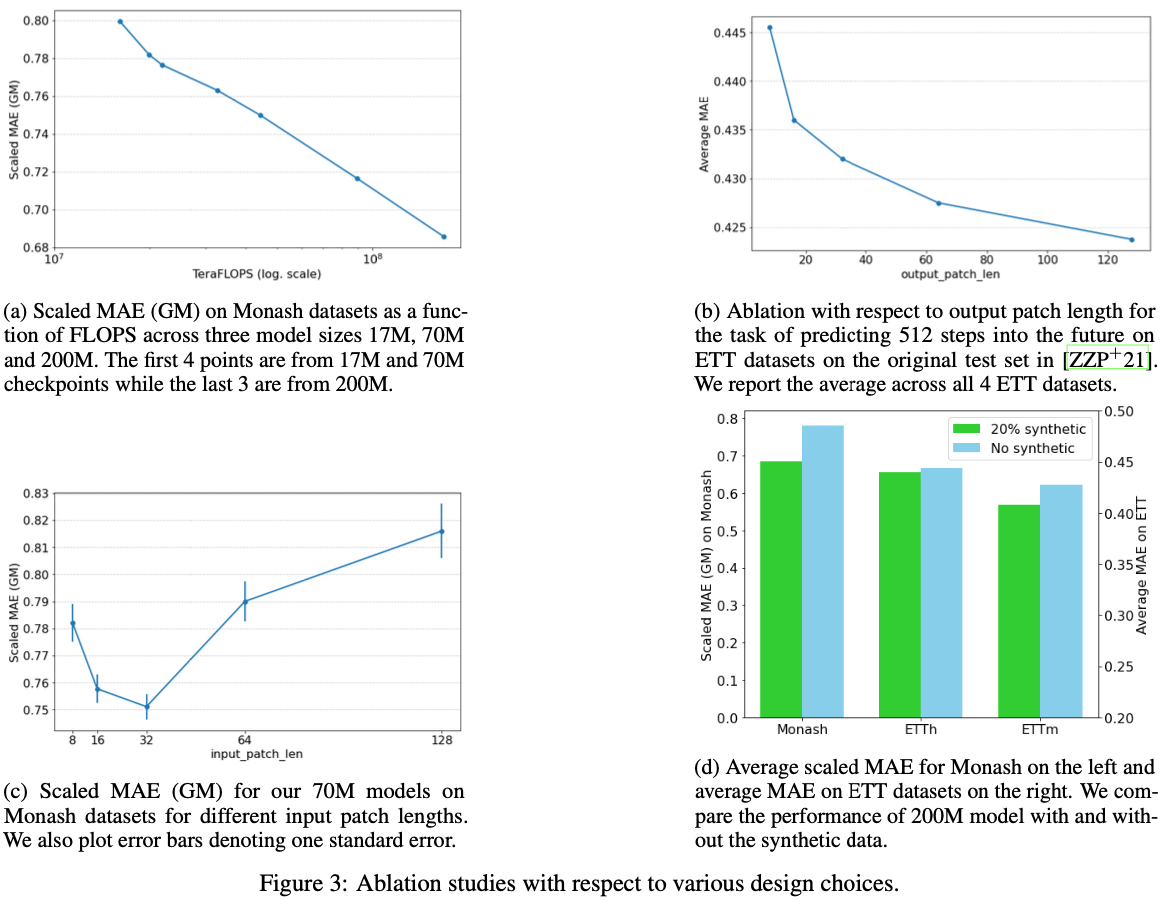
Scaling
- 파라미터 수를 17M, 70M, 200M으로 증가시키면서 성능을 평가했습니다.
- 배치 사이즈 4096으로 150만 iteration을 학습했습니다.
Autoregressive Decoding
- 긴 호라이즌을 한 번에 예측하는 것이 자기회귀 방식보다 더 나은 성능을 보임을 확인했습니다.
- input_patch_len보다 output_patch_len을 더 길게 두어 학습시킨 모델이 더 적은 자기회귀를 필요로 했습니다.
Input Patch Length
- 입력 패치 길이가 16과 32일 때 가장 좋은 성능을 보였습니다.
- 입력 패치 길이가 너무 길어지면 인코더-디코더 구조가 필요해졌습니다.
- 70M 모델로 입력 패치 길이를 8~128까지 실험한 결과, 너무 길어지면 성능이 떨어짐을 확인했습니다.
Dataset Ablation
- 합성 데이터의 필요성을 평가했습니다.
- 합성 데이터를 포함했을 때 성능이 약간 더 향상되었습니다.
- 학습에 사용된 실제 데이터셋들은 주로 시간 단위와 일 단위 데이터가 많아, 분 단위와 연 단위 데이터 예측력이 떨어졌습니다.
- Monash와 ETTm(15분)에서는 성능 향상이 뚜렷했으나, ETTh에서는 거의 동일했습니다.
결론
TimesFM 모델은 다양한 도메인의 시계열 데이터를 기반으로 학습되어 제로샷 예측에서도 우수한 성능을 발휘합니다. 패치 마스킹 전략과 긴 출력 패치 설정을 통해 효율성과 정확성을 높였으며, 이를 통해 다양한 시계열 예측 작업에서 높은 성능을 보여줍니다. TimesFM은 시계열 예측의 새로운 가능성을 열어주는 중요한 도구가 될 것입니다.
